Mathematics
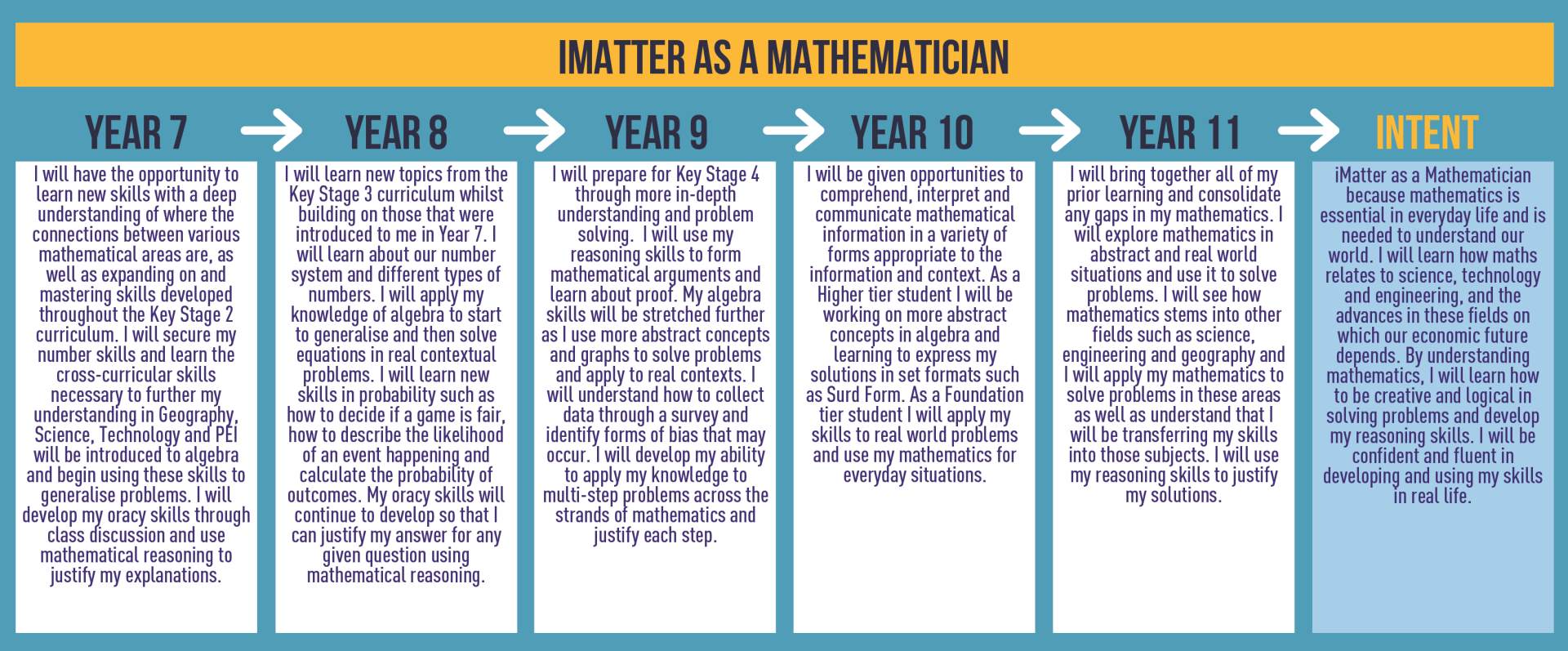
Year 7 Curriculum plans
| Term | What are we learning? | What Knowledge, Understanding and Skills will we gain? | What will excellence look like? | How will these be assessed? |
|
Autumn |
Place Value Calculations Data Time Coordinates |
Students will understand and use place value for decimals, measures and integers of any size. They will be able to round numbers and measures to an appropriate degree of accuracy. Students will recognise and use relationships between operations including inverse operations. They will use standard units of mass, length, time, money and other measures. Students will construct and interpret frequency tables, bar charts, and pictograms for categorical data, and vertical line or bar charts for ungrouped and grouped numerical data. Students will understand the (x,y) notation for coordinates and work with coordinates in all four quadrants. |
Students will be able to order positive integers and decimals; use the symbols =, ≠, , ≤, ≥. They will use approximation through rounding to estimate answers and calculate possible resulting errors expressed using inequality notation a Students will use the four operations, including formal written methods, applied to integers and decimals. They will use standard units of mass, length, time, money and other measures, including with decimal quantities. Students will be able to construct and interpret information in context from a variety of different graphical representations. Students will be able to apply their knowledge of coordinates in the cartesian plane to solve geometrical problems. |
These units will be assessed using formative assessment in class. The end of half-term assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Spring |
Negatives Fractions Indices Number Facts Order of Operations Introduction to Ratio |
Order negative integers and decimals; use the number line as a model for ordering of the real numbers; use the symbols =, ≠, , ≤, ≥. Use the four operations, including formal written methods, applied to integers and decimals, all both positive and negative. Express one quantity as a fraction of another, where the fraction is less than 1 and greater than 1. Order positive and negative fractions; use the number line as a model for ordering of the real numbers; use the symbols =, ≠, , ≤, ≥. Use the four operations, including formal written methods, applied to fractions. Use conventional notation for the priority of operations, including brackets, powers and roots. Use integer powers and associated real roots (square, cube and higher). Use the concepts and vocabulary of prime numbers, factors and multiples. Use ratio notation, including reduction to simplest form divide a given quantity into two parts in a given part:part or part:whole ratio; express the division of a quantity into two parts as a ratio. |
Apply knowledge of place value and the four operations to positive and negative integers and decimals. Use the four operations, including formal written methods, applied to proper and improper fractions, and mixed numbers, all both positive and negative. Conceptual understanding and fluency in the fundamentals of indices. Applying knowledge to solve more complex problems using the order of operations. Conceptual understanding and fluency in the fundamentals of prime numbers, factors and multiples. Use ratio notation and solve problems involving ratio. |
These units will be assessed using formative assessment in class. The end of half-term assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Summer |
Introduction to Algebra Shapes, Area and Pythagoras Perimeter |
Use and interpret algebraic notation. Substitute numerical values into expressions. Understand and use the concepts and vocabulary of expressions, equations, inequalities, terms and factors. Simplify and manipulate algebraic expressions. Use algebraic methods to solve linear equations in one variable. Derive and apply formulae to calculate and solve problems involving: perimeter and area of triangles, parallelograms, trapezia. Calculate and solve problems involving: perimeters of 2-D shapes (including circles), areas of circles and composite shapes. |
Understand and manipulate algebraic expressions. Solve linear equations in one variable. Reasoning and generalisation of algebraic problems. Identify properties and calculate the area and perimeter of 2-D shapes. Apply knowledge to solve geometrical problems. |
These units will be assessed using formative assessment in class. The end of half-term assessment will be marked by the teacher and recorded centrally for monitoring progress. |
Year 8 Curriculum plans
| Term | What are we learning? | What Knowledge, Understanding and Skills will we gain? | What will excellence look like? | How will these be assessed? |
|
Autumn |
Number Theory and Sequences
Functions, Co-ordinates and Graphs
Transformations
Fractions, Decimals, Percentages |
Use the concepts and vocabulary of highest common factor, lowest common multiple, prime factorisation, including using product notation and the unique factorisation property. Use integer powers and associated real roots. Appreciate the infinite nature of the sets of integers, real and rational numbers. Generate terms of a sequence from either a term-to-term or a position-to-term rule. Recognise arithmetic sequences and find the nth term. Recognise geometric sequences and appreciate other sequences that arise. Recognise, sketch and produce graphs of linear and quadratic functions of one variable with appropriate scaling, using equations in x and y and the Cartesian plane. Interpret mathematical relationships both algebraically and graphically. Reduce a given linear equation in two variables to the standard form y = mx + c; calculate and interpret gradients and intercepts of graphs of such linear equations numerically, graphically and algebraically.
Describe, sketch and draw using conventional terms and notations: points, lines, parallel lines, perpendicular lines, right angles, regular polygons, and other polygons that are reflectively and rotationally symmetric Identify properties of, and describe the results of, translations, rotations and reflections applied to given figures. Identify and construct congruent triangles, and construct similar shapes by enlargement, with and without coordinate grids.
Understand that a multiplicative relationship between two quantities can be expressed as a ratio or a fraction. Relate the language of ratios and the arithmetic of fractions. Convert between fractions, decimals, percentages and ratios. |
Conceptual understanding and fluency in the fundamentals of number theory. Reasoning and generalisation to solve mathematical problems involving sequences. Conceptual understanding and fluency in the fundamentals of graphing linear equations. Conceptual understanding and fluency in the fundamentals of the four transformations. Convert between fractions, decimals, percentages and ratios. |
These units will be assessed using formative assessment in class. The end of half-term assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Spring |
Introduction to Probability
Ratio, Proportion & Compound Measures
Expressions
Angles and construction |
Record, describe and analyse the frequency of outcomes of simple probability experiments involving randomness, fairness, equally and unequally likely outcomes, using appropriate language and the 0-1 probability scale. Understand that the probabilities of all possible outcomes sum to 1.
Understand that a multiplicative relationship between two quantities can be expressed as a ratio or a fraction Relate the language of ratios and the associated calculations to the arithmetic of fractions and to linear functions Solve problems involving direct and inverse proportion, including graphical and algebraic representations Use compound units such as speed, unit pricing and density to solve problems.
Use and interpret algebraic notation. Understand and use the concepts and vocabulary of expressions, equations, inequalities, terms and factors. Simplify and manipulate algebraic expressions to maintain equivalence by: collecting like terms; multiplying a single term over a bracket; taking out common factors; expanding products of two or more binomials. Draw and measure line segments and angles in geometric figures, including interpreting scale drawings Derive and use the standard ruler and compass constructions (perpendicular bisector of a line segment, constructing a perpendicular to a given line from/at a given point, bisecting a given angle); recognise and use the perpendicular distance from a point to a line as the shortest distance to the line. |
Mathematically reason, conjecture and justify the likelihood of different outcomes.
Apply knowledge of ratio and proportion to solve more complex mathematical problems. Generalise proportional relationships.
Conceptual understanding and fluency in the fundamentals of algebraic manipulation. Applying knowledge to solve more complex problems. Use mathematical equipment to construct accurate drawings. Apply this knowledge to solve more complex problems. |
These units will be assessed using formative assessment in class. The end of half-term assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Summer |
Angle facts
Formulae
Area & Volume
Form and Solve Equations |
Apply the properties of angles at a point, angles at a point on a straight line, vertically opposite angles Understand and use the relationship between parallel lines and alternate and corresponding angles. Derive and use the sum of angles in a triangle and use it to deduce the angle sum in any polygon, and to derive properties of regular polygons. Substitute numerical values into formulae and expressions, including scientific formulae. Understand and use standard mathematical formulae; rearrange formulae to change the subject.
Derive and apply formulae to calculate and solve problems involving: perimeter and area of triangles, parallelograms, trapezia, volume of cuboids (including cubes) and other prisms (including cylinders) Calculate and solve problems involving: perimeters of 2-D shapes (including circles), areas of circles and composite shapes Use the properties of faces, surfaces, edges and vertices of cubes, cuboids, prisms, cylinders, pyramids, cones and spheres to solve problems in 3-D. Model situations or procedures by translating them into algebraic expressions. Use algebraic methods to solve linear equations in one variable (including all forms that require rearrangement). Interpret mathematical relationships both algebraically and geometrically. |
Apply angle facts, triangle congruence, similarity and properties of quadrilaterals to derive results about angles and sides. Apply fundamentals of 2D shapes to solve more complex problems. Reasoning to solve multi-step problems. Apply knowledge of substitution to scientific formulae. Understand the link between mathematics and science and how these skills are applied in the wider world. Conceptual understanding and fluency in the fundamentals of area and volume. Reasoning to solve complex, multi-step problems. Applying fundamentals of algebraic manipulation to generalise mathematical relationships. Applying skills in wider context of geometry to solve more complex problems. |
These units will be assessed using formative assessment in class. The end of half-term assessment will be marked by the teacher and recorded centrally for monitoring progress. |
Year 9 Curriculum plans
| Term | What are we learning? | What Knowledge, Understanding and Skills will we gain? | What will excellence look like? | How will these be assessed? |
|
Autumn |
Fractions, Decimals & Percentages Standard Form Graphs |
Use standard units of mass, length, time, money and other measures, including with decimal quantities. Round numbers and measures to an appropriate degree of accuracy [for example, to a number of decimal places or significant figures]. Use approximation through rounding to estimate answers and calculate possible resulting errors expressed using inequality notation a Use a calculator and other technologies to calculate results accurately and then interpret them appropriately. Understand that a multiplicative relationship between two quantities can be expressed as a ratio or a fraction Solve problems involving percentage change, including: percentage increase, decrease and original value problems and simple interest in financial mathematics. Interpret and compare numbers in standard form A x 10n 1≤A. Model situations or procedures by translating them into algebraic expressions or formulae and by using graphs. Recognise, sketch and produce graphs of linear and quadratic functions of one variable with appropriate scaling, using equations in x and y and the Cartesian plane. Use linear and quadratic graphs to estimate values of y for given values of x and vice versa and to find approximate solutions of simultaneous linear equations. Find approximate solutions to contextual problems from given graphs of a variety of functions, including piece-wise linear, exponential and reciprocal graphs. |
Apply fundamentals of fractions, decimals and percentages to solve problems in the context of the wider world. Conceptual understanding and fluency in the fundamentals of standard form Apply knowledge in the wider context of science and technology. Conceptual understanding of a variety graphical functions. Apply knowledge to solving graphical problems in context of the wider world. |
These units will be assessed using formative assessment whilst being delivered. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Spring |
Angles and Similarity & Congruence Maps Scales Bearings Loci & Plans Pythagoras and Trigonometry |
Use the standard conventions for labelling the sides and angles of triangle ABC, and know and use the criteria for congruence of triangles. Use the properties of faces, surfaces, edges and vertices of cubes, cuboids, prisms, cylinders, pyramids, cones and spheres to solve problems in 3-D. Use scale factors, scale diagrams and maps. Draw and measure line segments and angles in geometric figures, including interpreting scale drawings. Derive and use the standard ruler and compass constructions (perpendicular bisector of a line segment, constructing a perpendicular to a given line from/at a given point, bisecting a given angle); Recognise and use the perpendicular distance from a point to a line as the shortest distance to the line. Use Pythagoras’ Theorem and trigonometric ratios in similar triangles to solve problems involving right-angled triangles. Use the properties of faces, surfaces, edges and vertices of cubes, cuboids, prisms, cylinders, pyramids, cones and spheres to solve problems in 3-D. |
Conceptual understanding of mathematical terminology and notation. Applying wider knowledge of shape to prove similarity and congruence and solve more complex problems. Fluency using mathematical instruments to create accurate drawings. Applying knowledge and reasoning to solve contextual problems. Conceptual understanding and fluency in the fundamentals of Pythagoras’ theorem and Trigonometry. Application of wider geometry skills to solve multi-step problems. |
These units will be assessed using formative assessment whilst being delivered. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Summer |
Probability Statistics Algebra Review |
Record, describe and analyse the frequency of outcomes of simple probability experiments involving randomness, fairness, equally and unequally likely outcomes, using appropriate language and the 0-1 probability scale. Understand that the probabilities of all possible outcomes sum to 1. Enumerate sets and unions/intersections of sets systematically, using tables, grids and Venn diagrams. Generate theoretical sample spaces for single and combined events with equally likely, mutually exclusive outcomes and use these to calculate theoretical probabilities. Describe, interpret and compare observed distributions of a single variable through: appropriate graphical representation involving discrete, continuous and grouped data; and appropriate measures of central tendency (mean, mode, median) and spread (range, consideration of outliers). Describe simple mathematical relationships between two variables (bivariate data) in observational and experimental contexts and illustrate using scatter graphs. Use and interpret algebraic notation, including. Substitute numerical values into formulae and expressions, including scientific formulae. Understand and use the concepts and vocabulary of expressions, equations, inequalities, terms and factors. Simplify and manipulate algebraic expressions to maintain equivalence by: collecting like terms; multiplying a single term over a bracket; taking out common factors; expanding products of two or more binomials. Understand and use standard mathematical formulae; rearrange formulae to change the subject. Model situations or procedures by translating them into algebraic expressions or formulae and by using graphs. Use algebraic methods to solve linear equations in one variable (including all forms that require rearrangement). |
Apply fundamentals of fractions, decimals and percentages in wider context of probability. Mathematically reason, conjecture and justify the likelihood of different outcomes. Plan and execute probability experiments. Mathematical understanding of the theoretical vs experimental probabilities. Analyse and interpret data in its wider context. Conjecture and justify relationships between two variables. Apply fundamentals of fractions, decimals and percentages in wider context of probability. Apply fundamentals of algebra to solve problems. Use reasoning skills to solve contextual problems. |
These units will be assessed using formative assessment whilst being delivered. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
Year 10 Curriculum plans
| Term | What are we learning? | What Knowledge, Understanding and Skills will we gain? | What will excellence look like? | How will these be assessed? |
|
Autumn |
Foundation: Number. Algebra. Graphs, tables and charts. Fractions and percentages. |
Students will revisit the key number facts and their uses. This includes calculations, decimal numbers, place value, factors, multiples and primes, squares, cubes and roots, index notation, prime factors. Students will revisit their algebraic manipulation techniques. This includes simplifying expressions, substitution, using formulae, expanding brackets, factorising, using expressions and formulae. Students will learn how data can be presented, displayed, interpreted and utilised. This includes frequency tables, two-way tables, representing data, time series, stem & leaf diagrams, pie charts, scatter graphs, line of best fit. Students will practise calculating with fractions, decimals and percentages. This will include working with fractions, operations with fractions, multiplying and dividing fractions, fractions and decimals, fractions and percentages, calculating percentages. |
Students will also be able to apply the algebraic techniques to solve worded and geometrical problems. Students will also be able identify why graphs may be misleading and demonstrate that they can interpret what all of these different charts and graphs show and answer questions in many real-life contexts. Students will also be able to calculate fluently using each of these skills to compare investments, solve budgeting problems and answer reasoning questions with correct justifications. |
These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Autumn |
Higher:Number.Algebra.Interpreting and representing data.Fractions, ratio and percentages. |
Students will revisit the key number facts and their uses. This will include solving number problems using reasoning, place value & estimation, HCF & LCM, calculating with indices, zero, fractional and negative indices, calculating in standard form, simplifying surds and rationalising the denominator.Students will revisit their algebraic manipulation techniques. This includes working with algebraic indices, expanding and factorising, solving equations, using and rearranging formulae, distinguishing between expressions, equations, formulae and identities, linear sequences, non-linear sequences, expand and factorise quadratics.Students will learn how data can be presented, displayed, interpreted and utilised. This includes drawing time series graphs, scatter graphs & LOBF, suitability of averages, averages and range of grouped data, two-way tables, misleading graphs.Students will practise calculating with fractions, decimals and percentages and ratios. This will include Calculating reciprocals, solve ratio problems, convert currencies & measures, direct proportion, percentage increases and decreases and real-life percentage problems. | Students will also be able to calculate fluently and solve problems in context using all of the skills gained.Students will also be able to apply these algebraic techniques to solve worded and geometrical problems.Students will also be able identify why graphs may be misleading and demonstrate that they can interpret what all of these different charts and graphs show and answer questions in many real-life contexts such as finance.Students will also be able to calculate fluently using each of these skills to compare investments, solve budgeting problems and answer reasoning questions with correct justifications. | These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Spring |
Foundation:Equations, inequalities and sequences.Angles.Averages and range. |
Students will develop their algebraic manipulation techniques, solving equations and inequalities, and working with sequences to solve problems. This will include solving linear equations, solving equations with brackets, introducing inequalities, solving inequalities, using formulae to solve equations, identify, equations, expressions, formulae and identities, generating sequences, nth term of a sequence.Students will use the angle properties of 2D shapes and parallel lines to solve problems. This will include angles in triangles, interior and exterior angles of polygons.Students will develop their further data handling techniques to present, display, calculate with and interpret data. This will include the mean & range from a list and frequency table, mode, median & range from a stem & leaf diagram, outliers, advantages and disadvantages of averages, estimate of mean, sampling and avoiding bias. | Students will also extend their use of all of these skills by solving problems with algebraic geometry, sequences, inequalities and solving equations from worded problems.Students will also confidently apply all the knowledge and skills to answer more complex geometrical problems.Students will also apply these techniques to analyse, interpret and comment on data that could occur in research, business and many other applications. They will also identify bias in data applications. | These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Spring |
Higher:Angles and trigonometry.Graphs.Area and volume.Transformations and constructions. |
Students will use angle properties of 2D shapes, Pythagoras’ Theorem and trigonometry to solve problems. This will include applying angle properties of triangles & quadrilaterals, interior & exterior angles of polygons, Pythagoras’ Theorem, trigonometry. angles of elevation & depression, know exact values of some trig ratios and use them to solve problems.Students will how to plot a range of different graphs accurately, demonstrating understanding and interpreting what is shown. This will include plotting linear graphs, finding the gradient, y-intercept, y=mx+c, graphing rates of change, work with line segments and plot quadratic graphs.Students will revisit how to calculate perimeter, area, volume and surface areas. This will include converting units of area and volume, accuracy & bounds, volume and SA of a prism, area & circumference of a circle, perimeter & area of sectors, volume & SA of cylinders, spheres, pyramids & cones.Students will learn to draw and interpret plans and elevations, scale drawings and bearings. They will perform transformations on 2D shapes and draw constructions accurately. | Students will also calculate angles of elevation & depression, know how to work out the exact values of some trig ratios without a calculator and use them to solve problems in context.Students will also be able to plot graphs of cubic & reciprocal graphs and identify their key features, draw and interpret linear & non-linear real-life graphs, draw the graph of a circle. Students will also apply these techniques to answering real life questions in different contexts. Students will also combine these skills to solve more complex geometrical problems algebraically as well as numerically.Students will also combine transformations, describe transformations fully and use their construction skills to solve problems on loci. They will learn how these techniques are used in construction and engineering to solve real-life problems. | These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Summer |
Foundation We are learning to calculate perimeter, area, convert units, volumes and surface areas. We are also learning about linear graphs and the equation of a straight line. We will also learn to transform a shape correctly on coordinate axes. |
Students will learn to calculate perimeter & area of rectangles, parallelograms, triangles & trapezia. Students will learn to convert units of area, calculate the area of compound shapes, volume and surface area of cuboids & prisms, converting units of volume. Students will learn to find the midpoint of a line, plot lines parallel to the axis, plot linear graphs, calculate gradient and the y-intercept and use it to find the equation of a line in the form y=mx+c. Students will also learn to draw and interpret real life graphs and distance-time graphs. Students will learn to translate a shape using a column vector, reflection, rotation and enlargement on a coordinate grid. They will learn to describe transformations and combine transformations. | Students will solve problems in context that require them to calculate perimeters, areas, volumes and surface areas of shapes. They will convert correctly between units of length, area and volume. Students will graphs of linear functions modelling real life scenarios, interpreting the gradient and y-intercept in context. They will be able to express the equation of the line in the form y=mx+c. Students will be able to interpret distance time graphs with different scales on the axes with accuracy. Students will be able to transform shapes correctly on a set of axes with all four quadrants. They will be able to describe transformations fully. They will combine transformations and then describe as a single transformation. | These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Summer |
Higher We are learning to solve quadratic equations, simultaneous equations and inequalities. We are learning about probability and how it is represented with diagrams and tables. We will then calculate using the rules of probability to solve problems. We are learning how to solve problems by applying multiplicative reasoning techniques. We are learning to recognise congruence and similarity and to apply our knowledge to solve problems. |
Students will learn to solve quadratic equations, use the quadratic formula and complete the square. Students will learn to solve simultaneous equations using algebraic methods. They will learn to solve linear inequalities and show solutions using set notation. Students will learn to calculate the probability of combined events, mutually exclusive events, experimental probability and independent events. Students will learn to use frequency trees and tree diagrams to calculate probabilities. They will learn to use Venn diagrams and set notation to represent probability. Students will learn how to calculate repeated percentage change for growth and decay. They will learn to convert metric speed measures and calculate with speed and acceleration. They will learn to solve problems with compound measures and solve problems with direct and indirect proportion. Students will learn the different conditions of congruence and proof and solve congruence problems. They will calculate the scale factors in similar shapes and calculate scale factors for areas and volumes. | Students will be able to select the correct method to use when solving quadratic equations. They will be able to apply this to questions in different contexts to find valid solutions. They will solve simultaneous equations where both are linear or there is one linear and one quadratic equation. They will solve inequalities and be able to show the solutions both on a number line or using set notation. Students will be able to solve a variety of complex probability problems including independent and dependent events. They will be able to use Venn diagrams and apply set notation to solving real life probability problems. Students will solve problems in context that involve repeated percentage change. They will be able to convert between different compound units and solve real life problems using various compound calculations including speed, density, pressure and rates of flow. They will recognise when to use different techniques to solve complex problems with direct and indirect proportion. Students will recognise the different conditions of congruence and proof and apply them to solve congruence problems. They will identify real life problems with similarity and calculate scale factors and solve problems with linear measures, areas and volumes. | These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
Year 11 Curriculum plans
| Term | What are we learning? | What Knowledge, Understanding and Skills will we gain? | What will excellence look like? | How will these be assessed? |
|
Autumn |
Foundation:Ratio and proportion.Right-angled triangles.Probability.Multiplicative reasoning. |
Students will use ratios and proportion numerically and graphically to solve problems. This will include writing & simplifying ratios, using ratios to solve problems, ratios & measures, divide a quantity in a given ratio, comparing unit ratios, using proportion to solve problems, direct proportion & graphs, direct & indirect proportion problems.Students will use Pythagoras’ Theorem and trigonometry. This will include calculating an unknown side length or a line segment, use trigonometry, sin, cos & tan to calculate a side or an angle.Students will learn how to apply the rules of probability. This will include calculating simple probabilities, two-way tables for recording two events and calculating experimental and expected probabilities.Students will use multiplicative reasoning, percentage changes and proportion to solve problems. This will include percentage calculations for profit & loss, original amounts, growth & decay for compound calculations, compound measures, distance, speed & time calculations, convert units of speed, calculate acceleration, direct and inverse proportion problems. | Students will use of these skills and apply them to answer questions on value for money and other problem-solving and modelling questions.Students will also know how to work out the exact value of sin, cos or tan of some angles without a calculator. They will apply this knowledge to solving more challenging geometrical problems.Students will also solve probability problems using Venn diagrams & set language, frequency trees & probability trees. They will understand how to calculate probabilities of independent events and solve problems with non-independent events.Students will also be able to apply their knowledge of compound measures, direct and inverse proportion to solve real-life problems of increasing complexity. | These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Autumn |
Higher:More trigonometry.Further statistics.Circle theorems.Equations and graphs. |
Students will learn how bounds affect the accuracy of solutions. They will graph the trigonometric functions and calculate using further trig equations to solve problems. This will include using accuracy & bounds, graphs of trig functions, area of a triangle & segment, use of sine and cosine rule, bearings using trigonometry.Students will learn how to manipulate data, plot a range of different graphs and charts accurately, demonstrating understanding and interpreting what is shown. This will include learning about random & stratified sampling, cumulative frequency tables & diagrams, median, quartiles & IQR, stem & leaf diagrams, draw & interpret box plots. Students will learn and apply the circle theorems to solve problems. This will include solving problems with radii & chords, problems with tangents, using & applying all circle theorems to solve problems.Students will use further algebraic manipulation techniques including iteration, solving quadratics and cubic equations graphically. This will include representing inequalities graphically, plotting graphs of quadratic functions, solving quadratic equations graphically, plotting graphs of cubic functions & finding the roots. | Some pupils will also learn to apply 3D Pythagoras and 3D trigonometry, and to plot trigonometric graphs and transformations of these trigonometric graphs.Students will also calculate frequency density to draw histograms, compare & describe populations. They will apply all of these data handling techniques to answer complex questions about data and to form opinions about what the data is showing and how this can be interpreted in the real world.Students will also be combining several circle theorems and using mathematical language and reasoning to explain and give reasons for their solutions to geometrical problems.Students will be able to apply all of these further algebraic manipulation techniques including iteration to solve equations. They will also be able to solve quadratic inequalities algebraically and sketch a graph to show the solutions. | These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress. |
|
Spring |
Foundation:Constructions, loci and bearings.Quadratic equations and graphs.Perimeter area and volume 2.Fractions, indices and standard form.Congruence, similarity and vectors.More algebra. |
Students will learn to draw and interpret plans and elevations, scale drawings and bearings and draw constructions. This will include representing 3D solids by drawing plans & elevations, accurate drawings, scale drawings & maps, constructions, loci & regions, bearings.Students will learn more algebraic manipulation techniques, solving equations algebraically and graphically. This will include expanding double brackets, plotting quadratic graphs, using quadratic graphs, factorising quadratics, solving quadratics graphically & algebraically.Students will learn additional techniques to calculate perimeter, area, volume and surface areas to solve problems. They will calculate circumference & radius of a circle, area of a circle, area & perimeter of semicircles & sectors, area of composite 2D shapes.Students will learn more methods of calculating with fractions and indices. They will multiply and divide with fractions and mixed numbers, use the laws of indices.Students will learn the conditions for congruence, similarity, calculate scale factors, enlargement and learn to calculate simple vectors sums.Students will learn how to plot a range of graphs accurately, demonstrating understanding and interpreting what is shown. This will include plotting graphs of cubic & reciprocal functions, non-linear graphs, rearranging formulae, algebraic proof. | Students will be able to combine the skills learned with constructions to solve complex problems with loci and bearings in context.Students will be able to apply these algebraic manipulation techniques to answers complex GCSE exam questions correctly.Students will also calculate the volume and surface area of cylinders, pyramids, cones & spheres, volume & SA of composite 3D solids. They will use these to solve problems in context.Students will also be able to write numbers in standard form and solve problems by calculating with standard form.Students will also apply their knowledge to recognise and draw congruence and similarity, draw enlargement with fractional scale factors, calculate a scale factor, Students will learn to add & subtract vectors and find multiples of vectors.Students will also write and solve simultaneous equations using graphical and algebraic methods and develop their algebraic manipulation and knowledge of proof to solve problems. | These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress.Mock exams with Paper 1, Paper 2 and Paper 3 will provide an accurate GCSE grade and allow a predicted grade to be determined. |
|
Spring |
Higher:More algebra.Vectors and geometric proof.Proportional graphs. |
Students will learn further algebraic manipulation techniques with algebraic fractions and surds to solve problems. This will include addition, subtraction, multiplying, division & simplifying of algebraic fractions. Students will also learn to simplify and expand surds and how and why we rationalise the denominator.Students will draw vectors and apply vector arithmetic and use proof to solve problems. This will include use of vector notation, and calculation using vector arithmetic.Students will learn how to solve problems using algebraic proportionality. They will learn how to plot graphs of functions and understand how to transform them. This will include writing equations to solve problems with direct proportion, square & cubic proportionality, inverse proportion problems and graphs. | Students will also be able to use of function notation, find composite & inverse functions and show algebraic proof. Students will also be able to use parallel vectors & collinear points, solving geometric problems & justifying with vector proof.Students will also be able to plot graphs of exponential functions, non-linear graphs and calculate the gradient of a tangent. They will translate graphs of functions, including reflecting & stretching graphs of functions. | These units will be assessed using formative assessment whilst being delivered. Past GCSE exam questions will be used within lessons and with the weekly homeworks. The end of unit assessment will be marked by the teacher and recorded centrally for monitoring progress.Mock exams with Paper 1, Paper 2 and Paper 3 will provide an accurate GCSE grade and allow a predicted grade to be determined. |